Tudom-tudom, a matematika szótól a legtöbb embernek égnek áll a haja. Ennek nyilván az az oka, hogy sokan nem értik, vagy anno nem tanították meg jól és az elmaradt sikerélmény és a rossz osztályzatok miatt inkább utálat (tan)tárgya lett. Márpedig a matek nagyon jó, főleg, hogy bármennyire is hihetetlen, a mindennapi életben remekül lehet alkalmazni.

Nem térek ki az összes pozitív tulajdonságára, miszerint a matematika gyakorlásával remekül lehet pl. az agyat tornáztatni és frissen tartani, így talán később ér el a korral együtt járó feledékenység… Fejleszti a logikát, a megoldókészséget, és még akkor is, ha ténylegesen nem egy exponenciális vagy trigonometrikus egyenlet lesz egy adott problémára a megoldás, sok tekintetben hozzásegít felmerülő problémák hatékonyabb, gyorsabb, precízebb megoldásához.
Nem véletlenül van az a mondás sem, hogy „többet ésszel, mint erővel”. Ha csak a lakberendezésre szorítkozunk, nekem számtalanszor fordult már elő a munkám során, hogy alap matematikával kiszámoltam, miképpen rendezhető be egy tér papíron adott bútorokkal anélkül, hogy a helyszínen lennénk, vagy magukat a bútorokat megmozdítanánk. Jól jön csempemennyiségek, festékadagok számolásakor, vagy hogy éppen mennyi járólap, laminált, stb. szükséges, hogy ne vegyünk keveset, de túl sokat sem. A matematikával nagyon jól lehet ilyen tekintetben spórolni is.
Legutóbb Noémi Barátnőm (Kedvenc Otthon) írt rám egy lakberendezési kérdést megvitatni, mely szerint milyen mélységet igényel egy ilyen cipőtárolós szekrény:
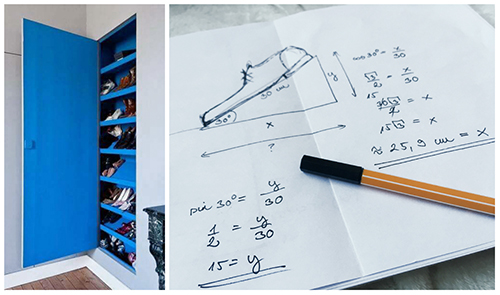
Derékszögű háromszögekre vonatkozó alap trigonometria összefüggéssel ez tényleg 1 perc alatt kényelmesen kiszámolható, úgyhogy gyorsan megszületett a kérdésre a válasz. Persze, nem csak ez az egy mód van, le lehet modellezni kartonnal és mérőszalaggal / vonalzóval is ki lehet matekozni, de ha van rá egy precíz „eszközünk”, akkor miért ne lehetne azzal.
Egyszer már írtam amúgy a matek gyakorlati alkalmazásáról itt a blogon, amikor egy szabályos háromszögekkel mintázott lámpaernyőt festettem, ITT.

De visszanézve a blogot, számos példát találtam arra, ahol a középsuliban megszerzett tudást remekül hasznosítottam:
Amikor pl. a dobogót terveztem (ITT), addig kalkuláltam, míg ki nem jött a legoptimálisabb megoldás, amivel a legkevesebb lehulló maradék keletkezik és amivel a projekt költségét is minimalizálom.

Jól jött akkor is, amikor az inspirációs fal sablonját terveztem (ITT) vagy amikor a geometrikus betűzőt készítettem (ITT).


A hexagon (szabályos hatszög) amúgy is nagy kedvencem, legutóbb márványmintás poháralátéteket készítettem belőlük (ITT).

Térbeli elemeknél pedig pláne hasznos volt a geometria, pl. a menő szögletes „bronz” vázámnál (ITT) és az ikozaéder lámpámnál is (ITT).


Szóval a matematika hasznos, és igenis menő érteni és használni. Nekem szerencsém volt, mert mind az általános iskolás tanárnőm (Sárkány Zsuzsa néni), mind pedig a gimnáziumi évek alatti tanáraim (Smejkál Szilvia és Gyulay Éva tanárnő, utóbbinál vért izzadtam, de örök hála neki, a kemény, személyreszabott feladatokért!) kiváló, lelkiismeretes pedagógusok voltak, meg hát nyilván otthon Apukám is zseni a témában – még most, 71-en túl is -, így könnyű volt felszippantanom a tudást.
Most például ezeket olvasom, és baromi érdekes – nem csak matematikai – dolgok vannak bennük:

Szerintem tök jó lenne, ha a szakközépben illetve gimnáziumban megtanultak (tehát egy középfokú, érettségi szint) megmaradna a fejünkben… 40-hez közeledve azért érzem, hogy amit nem használ az ember, az erősen meg tud kopni, bár ennek kompenzálására és új tudás megszerzésére remek módszereim vannak, ami szerintem szintén megér egy blogposztot.
Nektek melyik tantárgy megy a mai napig jól?




Igen, a matek tudás bizony sokszor hasznosnak bizonyul, amikor valamit alkotni szeretnél 🙂
Hm, a geometrikus posztjaid, illetve a végeredményük nem egyszer lenyűgözőek, de az alkalmazott tudás mellett nem kis türelem is kell több művedhez.
Nekem sose volt gondom a matekkal v. alkalmazásával, de bizony egyrészt kell hozzá érzék/tehetség, másrészt gyakran nem jól oktatják. Mit értek ezen? Azt, hogy amit ki tud valaki számolni elméletben képletekkel, azt nem tudja gyakorlatban alkalmazni, mert nem ismeri fel (nem jön rá), hogy ide ez vagy az, az általa egyébként ismert képlet/módszer alkalmazandó. Ezt egyébként a nemzetközi PISA tesztek is kimutatják.
„Amikor pl. a dobogót terveztem (ITT), addig kalkuláltam, míg ki nem jött a legoptimálisabb megoldás, amivel a legkevesebb lehulló maradék keletkezik és amivel a projekt költségét is minimalizálom.”
Félve írom hogy ne kötekedésnek hasson :), de az optimális önmagában azt jelenti h. legjobb, legkedvezőbb, igy sem közép, sem felsőfoka nem lehet – csak nyelvtanilag.
Jogos, ezentúl majd figyelek rá.
„40-hez közeledve azért érzem, hogy amit nem használ az ember, az erősen meg tud kopni, bár ennek kompenzálására és új tudás megszerzésére remek módszereim vannak, ami szerintem szintén megér egy blogposztot.”…
Hát, nagyon kíváncsi lennék a tippekre 🙂 Várom a posztot róla!
Milyen jó, hogy írtál, mert ezt a jó kis témát már el is felejtettem. Haha, ilyen ez a közelgő 40 😀